Enotni vektorski zapis | Vektorji in prostori | Linearna algebra | Khan Academy
Ko razlagajo dimenzijo W, je ta predstavljena kot negativna stran osi X. Zakaj je dimenzija W negativna X? Ali res ni to lastna dimenzija?

- Poskusite risati 4-dimenzionalni graf na dvodimenzionalno površino. To so si izmislili (vaša pravica, čeprav ni dober graf).
Kot je omenil @NendoTaka, je na dvodimenzionalni površini precej težko narisati 4d objekt.
Tako deluje dimenzionalnost:
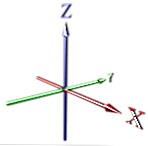
z eno dimenzijo se točka pošlje neskončno in ustvarja črto (glej X)
v 2d dodamo dimenzijo pravokotno na to (glej X, Y).
Nato gremo spet pravokotno in se razširimo navzgor, da dobimo tretjo dimenzijo (glej X, Y, Z).
Ker je 3d> 2d, ne moremo tako dobro predstaviti papirja, ne da bi ga prepognili ali dodali več listov nanj - vse to je za ogled na zaslonu res nepraktično. Namesto tega uporabljamo perspektivo - kako naše oči dojemajo 3d. Običajno so koti tukaj ~ 30 stopinj.

In to se zdi precej v redu, ker naše oči ne vidijo v tem tradicionalnem 3D pomenu, tako posnemanje, ki deluje. Ko pa želimo predstavljati 4. dimenzijo, tega nimamo s čim primerjati. Ponovno moramo iti pravokotno in to naše oči težko razumemo, saj nimamo veliko reference.
Tu je primer upodobitve 4. dimenzije:
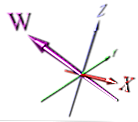
To je pravilnejši način prikaza dimenzije, vendar se vseeno zanaša na perspektivo - tudi ni takoj očitno, da gre na prvi pogled za novo dimenzijo.
Verjetno so se animatorji odločili za nekaj preprostega, kar bi bilo lažje animirati. Če bi zasukali zgornjo sliko, bi se dimenziji X in W lahko prekrivale - in to ne bi bilo očitno na sliki brez kazalcev puščic.
Torej, ja, motijo se - vendar tudi ni preprostega načina predstavitve 4 dimenzij na enem listu papirja
Usklajeni viri slik in dobro branje
3- 1 Po pravici povedano obstaja veliko standardnih načinov projiciranja 4-dimenzionalnih predmetov, kot so tesseracts in 3-krogle v 3 dimenzije (in nato na običajne načine do 2 dimenzij), ki so precej boljši od tistega, ki se uporablja v oddaji, mnogi od katerih imajo dodaten bonus videti hladnejši od tistega, uporabljenega v oddaji.
- @senshin oh zagotovo, ampak mislim, da so tudi animatorji želeli nekaj razložiti, ne pa presenetiti
- 1 Poleg položaja lahko uporabite druge stvari, da označite, kako daleč vzdolž osi je nekaj, na primer barva.